2024. 5. 4. 04:35ㆍ수학
이전 글에서 언급했다시피
벡터는 위치와 방향, 그리고 그 방향으로 작용하는 힘의 크기를 담고 있다
이번에는 벡터의 합차를 알아보자
우선 벡터의 합이다
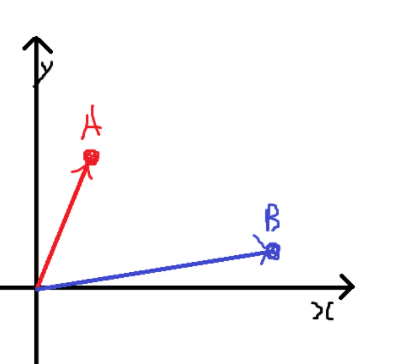
합 연산을 해야 하기 때문에 두 개의 벡터를 만들어준다

위와 같은 벡터들을 추가하고 나서 대충 비유를 통해 설명을 해보자면
(0, 0)에 있는 한 물체를 저 두 벡터의 방향으로 일정하게 당기는 것과 같다

그럼 결론적으로는 노란색 화살표의 방향으로 당겨지는 것과 같다
이런 식으로 평행 사변형을 그려서 벡터의 합을 설명한다
이것을 어떻게 활용할 수 있을까?
일반적으로 벡터 합은 기준위치에서 얼마만큼 이동했는 지를 계산 할 수 있다.
이게 무슨 말이냐 하면
A라는 점을 기준으로 원을 그려 원중의 한 점을 랜덤으로 선택했다

이러면 A로부터 떨어진 만큼의 A를 기준으로 한 벡터로 B의 위치를 알 수 있을 것이다.
하지만 이것은 어디까지나 A를 기준으로 한 로컬 좌표계(상대좌표)의 기준이고
이를 월드 좌표계(절대좌표)로 구하기 위해서는 B의 로컬 좌표벡터에 A의 월드좌표 벡터를 더하면 된다.

이런 식으로 B의 로컬 좌표계를 월드로 옮겨 0,0을 기준으로 그려주고
A벡터와 벡터합을 해주면 B의 월드좌표 벡터를 얻을 수 있다
(노란색 선이 결과적으로 B의 월드벡터이다)
다음은 벡터의 차이다
벡터의 차 연산은 게임개발에서 보통 벡터 합 보다 더 많이 사용하게 되는 연산이다.
왜냐하면 이것은 더 벡터 간의 차.
즉, 거리를 포함한 A에서 B지점의 방향을 알 수 있다
간단하게 설명하자면 벡터 차는
(A벡터) - (B벡터) => (B -> A의 방향벡터)
라고 생각하면 된다

따라서 그냥 이렇게 된다
(초록색 벡터가 B에서 A의 방향벡터를 의미한다)
이런식으로 사용하는 벡터의 차는
한 지점에서 다른지점의 방향을 구한다는 점에서 게임 개발에서는 많이 사용할 수밖에 없는 것이다.
예를 들기에도 너무나 많은것이,
방향을 구하는 연산이 필요한 곳에는 무조건적으로 사용하는 연산이라 조준한 방향으로
총을 쏠 때의 방향을 알아내는 데나 적이 플레이어를 감지하거나 감지하여 따라올 방향을
제시하는 등등에 사용한다.
